Source data: nakji.network
Introduction
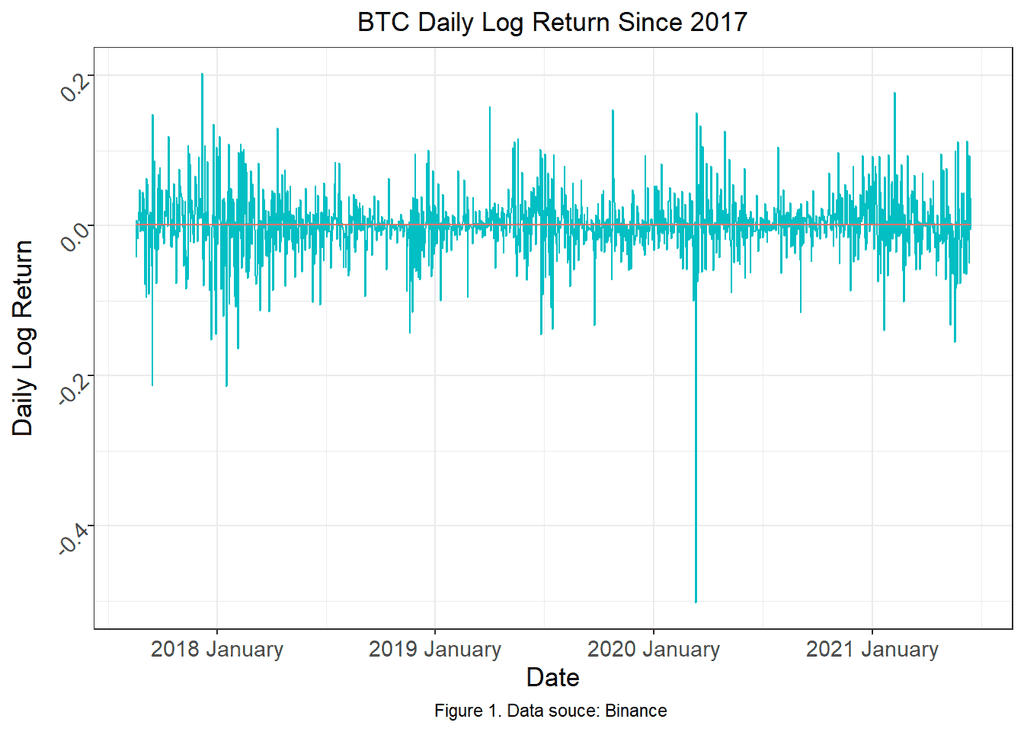
Bitcoin is a decentralized digital currency that can be sent from user to user on the Bitcoin network without a central bank. Studies have been focused on predicting its price and volatility. However, investors are mostly concerned about Bitcoin’s rate of return for their investments. With this in mind, our analysis mainly focuses on the daily log return of the Bitcoin price from August 2017 to June 2021. This study uses the log return on the ground that stock price is assumed to be log normally distributed, and we use a similar assumption for the Bitcoin price.
Daily Log Return
Figure 1 shows the daily log return of BTC in USD. From the plot, it seems that the return fluctuates around the mean daily log return, which is 0.157, shown as the red line. Although we cannot make a conclusion simply by looking at the plot, the BTC daily log return may have a seasonal pattern where it fluctuates around the mean within a seemingly fixed interval. It is worth pointing out that the change in variance of the data is obvious. Especially around January of 2020, the log return sharply dropped to -0.5 and soon recovered. To examine the seasonality and pick the suitable model, we need to look at the ACF and PACF plot.
ACF and PACF plots
Figure 2 shows the autocorrelation plot of the BTC daily log return. The red lines mark the (+/-) significance level to check whether the ACF coefficient at a given time lag is significantly different from 0. An autocorrelation plot explains how the present value of the time series data is correlated with the past values under different time lags. By looking at the plot, there is no strong pattern of the significant ACF coefficients in a given fixed interval. Thus, we can conclude that there is not a strong seasonality in the BTC daily log return data.
Figure 3 shows the partial autocorrelation plot of the BTC daily log return. Similarly, the red line marks the (+/-) significance level to check whether the PACF coefficient at a given time lag is significantly different from 0. A Partial Autocorrelation plot shows the correlation between the parts of the present value of the time series data and the value of a given time lag that are not predicted by the values of the other time lags. To determine which model to fit, it is necessary to make sure that the given time series data is stationary. By ‘stationary’, it assumes that the mean, variance, and the autocorrelation of the given time series data do not change over time. To test for stationarity, we perform an Augmented Dickey-Fuller Test.
Augmented Dickey-Fuller Test
data: data_bitcoin$log_return
Dickey-Fuller = -10.027, Lag order = 11, p-value = 0.01
alternative hypothesis: stationaryThe test result shown above is an Augmented Dickey-Fuller (ADF) Test on stationarity. Based on the ADF Test, the Null hypothesis is that there is unit-root presented in the autoregression model. Having the unit-root is a sign that the time series data has a stochastic trend that introduces non-stationarity into the data. The Alternative hypothesis is that there is stationarity presented in the data. Since the p-value is 0.01, we reject the Null hypothesis that there is unit-root presented in the data, and we may conclude that the BTC daily log return is stationary. Thus, the ARMA model is suitable for the given time series data. To test if we need to implement a GARCH model, a Ljung-Box test is performed.
Test on Garch Effect
| Test statistic | df | P value |
|---|---|---|
| 23.77 | 12 | 0.02184 * |
The Null hypothesis of the Ljung-box test is that the first few lags of the ACF of the variance series are statistically zero. Based on the test above, we have a p-value 0.021 which is smaller than 0.05. Thus we reject the Null hypothesis and conclude that there is a GARCH effect in the given time series data. By Figure 2 and Figure 3, because of the wave shape of the ACF plot and that the first spike of PACF is statistically non-zero, we would consider AR(1), and ARMA(1,1). To pick the order of the GARCH model, we plot the EACF to find the candidates.
AR/MA
0 1 2 3 4 5 6 7 8 9 10 11 12 13
0 x x o o o o o o o x o o o o
1 x x o o o o o o o x o o o o
2 x o o o o o o o o x o o o o
3 x o x o o o o o o x o o o o
4 x x x x o o o o o x o o o o
5 x x x x o o o o o x o o o o
6 x x x x x o o o o x o o o o
7 x x x x x x o o o o o o o oBased on the EACF table, we would consider the GARCH(2,1) and GARCH(1,2) models.
Model Estimation
Title:
GARCH Modelling
Call:
garchFit(formula = ~arma(0, 1) + garch(2, 1), data = data_bitcoin$log_return,
cond.dist = "norm", trace = F)
Mean and Variance Equation:
data ~ arma(0, 1) + garch(2, 1)
<environment: 0x000000001f1b8718>
[data = data_bitcoin$log_return]
Conditional Distribution:
norm
Coefficient(s):
mu ma1 omega alpha1 alpha2 beta1
0.00176973 -0.03309070 0.00011100 0.16189402 0.00000001 0.79141081
Std. Errors:
based on Hessian
Error Analysis:
Estimate Std. Error t value Pr(>|t|)
mu 1.770e-03 9.233e-04 1.917 0.0553 .
ma1 -3.309e-02 2.940e-02 -1.125 0.2604
omega 1.110e-04 2.781e-05 3.991 6.59e-05 ***
alpha1 1.619e-01 3.544e-02 4.569 4.91e-06 ***
alpha2 1.000e-08 4.626e-02 0.000 1.0000
beta1 7.914e-01 3.959e-02 19.990 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Log Likelihood:
2525.208 normalized: 1.80372
Description:
Tue Jul 13 02:21:14 2021 by user: Henry
Standardised Residuals Tests:
Statistic p-Value
Jarque-Bera Test R Chi^2 754.7275 0
Shapiro-Wilk Test R W 0.9524657 0
Ljung-Box Test R Q(10) 17.42951 0.06538402
Ljung-Box Test R Q(15) 20.27546 0.1616186
Ljung-Box Test R Q(20) 23.65651 0.2577187
Ljung-Box Test R^2 Q(10) 7.195612 0.706858
Ljung-Box Test R^2 Q(15) 8.720435 0.8916755
Ljung-Box Test R^2 Q(20) 13.21738 0.8678636
LM Arch Test R TR^2 7.624555 0.8137392
Information Criterion Statistics:
AIC BIC SIC HQIC
-3.598868 -3.576393 -3.598905 -3.590467Title:
GARCH Modelling
Call:
garchFit(formula = ~arma(0, 1) + garch(1, 2), data = data_bitcoin$log_return,
cond.dist = "norm", trace = F)
Mean and Variance Equation:
data ~ arma(0, 1) + garch(1, 2)
<environment: 0x00000000244c4870>
[data = data_bitcoin$log_return]
Conditional Distribution:
norm
Coefficient(s):
mu ma1 omega alpha1 beta1 beta2
0.00169063 -0.03683076 0.00013681 0.19696944 0.45766408 0.28640742
Std. Errors:
based on Hessian
Error Analysis:
Estimate Std. Error t value Pr(>|t|)
mu 1.691e-03 9.153e-04 1.847 0.06474 .
ma1 -3.683e-02 2.987e-02 -1.233 0.21756
omega 1.368e-04 3.181e-05 4.301 1.70e-05 ***
alpha1 1.970e-01 3.558e-02 5.536 3.09e-08 ***
beta1 4.577e-01 1.570e-01 2.914 0.00356 **
beta2 2.864e-01 1.358e-01 2.109 0.03494 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Log Likelihood:
2526.187 normalized: 1.804419
Description:
Tue Jul 13 02:21:14 2021 by user: Henry
Standardised Residuals Tests:
Statistic p-Value
Jarque-Bera Test R Chi^2 707.0289 0
Shapiro-Wilk Test R W 0.9530929 0
Ljung-Box Test R Q(10) 17.48786 0.06424225
Ljung-Box Test R Q(15) 20.20186 0.164325
Ljung-Box Test R Q(20) 23.6744 0.2569046
Ljung-Box Test R^2 Q(10) 6.571882 0.7651488
Ljung-Box Test R^2 Q(15) 8.050817 0.9217292
Ljung-Box Test R^2 Q(20) 12.63901 0.8923298
LM Arch Test R TR^2 6.81881 0.8693513
Information Criterion Statistics:
AIC BIC SIC HQIC
-3.600267 -3.577792 -3.600304 -3.591866Title:
GARCH Modelling
Call:
garchFit(formula = ~arma(1, 1) + garch(2, 1), data = data_bitcoin$log_return,
cond.dist = "norm", trace = F)
Mean and Variance Equation:
data ~ arma(1, 1) + garch(2, 1)
<environment: 0x0000000026f28a60>
[data = data_bitcoin$log_return]
Conditional Distribution:
norm
Coefficient(s):
mu ar1 ma1 omega alpha1 alpha2
0.00244564 -0.38905336 0.33890888 0.00011016 0.16023529 0.00000001
beta1
0.79311816
Std. Errors:
based on Hessian
Error Analysis:
Estimate Std. Error t value Pr(>|t|)
mu 2.446e-03 1.346e-03 1.817 0.0692 .
ar1 -3.891e-01 2.403e-01 -1.619 0.1054
ma1 3.389e-01 2.436e-01 1.391 0.1642
omega 1.102e-04 2.760e-05 3.991 6.58e-05 ***
alpha1 1.602e-01 3.508e-02 4.567 4.94e-06 ***
alpha2 1.000e-08 4.591e-02 0.000 1.0000
beta1 7.931e-01 3.945e-02 20.103 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Log Likelihood:
2526.022 normalized: 1.804302
Description:
Tue Jul 13 02:21:14 2021 by user: Henry
Standardised Residuals Tests:
Statistic p-Value
Jarque-Bera Test R Chi^2 776.544 0
Shapiro-Wilk Test R W 0.9522576 0
Ljung-Box Test R Q(10) 14.4061 0.1552609
Ljung-Box Test R Q(15) 17.15823 0.3094939
Ljung-Box Test R Q(20) 20.55216 0.4238998
Ljung-Box Test R^2 Q(10) 7.213481 0.705149
Ljung-Box Test R^2 Q(15) 8.873923 0.8840168
Ljung-Box Test R^2 Q(20) 13.21939 0.8677737
LM Arch Test R TR^2 7.724762 0.8062525
Information Criterion Statistics:
AIC BIC SIC HQIC
-3.598603 -3.572382 -3.598653 -3.588801</code></pre>Title:
GARCH Modelling
Call:
garchFit(formula = ~arma(1, 1) + garch(1, 2), data = data_bitcoin$log_return,
cond.dist = "norm", trace = F)
Mean and Variance Equation:
data ~ arma(1, 1) + garch(1, 2)
<environment: 0x00000000246e0420>
[data = data_bitcoin$log_return]
Conditional Distribution:
norm
Coefficient(s):
mu ar1 ma1 omega alpha1 beta1
0.00233039 -0.39372369 0.33805756 0.00013727 0.19679464 0.44290573
beta2
0.30068935
Std. Errors:
based on Hessian
Error Analysis:
Estimate Std. Error t value Pr(>|t|)
mu 2.330e-03 1.325e-03 1.759 0.07858 .
ar1 -3.937e-01 2.237e-01 -1.760 0.07841 .
ma1 3.381e-01 2.276e-01 1.486 0.13738
omega 1.373e-04 3.177e-05 4.320 1.56e-05 ***
alpha1 1.968e-01 3.536e-02 5.566 2.60e-08 ***
beta1 4.429e-01 1.525e-01 2.904 0.00369 **
beta2 3.007e-01 1.322e-01 2.274 0.02298 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Log Likelihood:
2527.131 normalized: 1.805093
Description:
Tue Jul 13 02:21:14 2021 by user: Henry
Standardised Residuals Tests:
Statistic p-Value
Jarque-Bera Test R Chi^2 723.4335 0
Shapiro-Wilk Test R W 0.9529311 0
Ljung-Box Test R Q(10) 14.30139 0.1596828
Ljung-Box Test R Q(15) 16.91757 0.3238159
Ljung-Box Test R Q(20) 20.40143 0.4330832
Ljung-Box Test R^2 Q(10) 6.556995 0.7665002
Ljung-Box Test R^2 Q(15) 8.178631 0.9164215
Ljung-Box Test R^2 Q(20) 12.62734 0.8927946
LM Arch Test R TR^2 6.86487 0.8664127
Information Criterion Statistics:
AIC BIC SIC HQIC
-3.600187 -3.573965 -3.600236 -3.590385From the Information Criterion Statistics, we can make comparisons between the models by measuring the prediction error based on Akaike Information Criterion (AIC) score. By comparing the AIC score of the fitted models, the ARMA(0,1)+GARCH(1,2) is preferred.
The Selected Model and Model diagnostic
From the QQ plot, we see that on both of the tails, the data points largely deviate from the normality line. This implies that the normality assumption of the GARCH model on its residuals may be violated.
Title:
GARCH Modelling
Call:
garchFit(formula = ~arma(0, 1) + garch(1, 2), data = data_bitcoin$log_return,
cond.dist = "norm", trace = F)
Mean and Variance Equation:
data ~ arma(0, 1) + garch(1, 2)
<environment: 0x00000000244c4870>
[data = data_bitcoin$log_return]
Conditional Distribution:
norm
Coefficient(s):
mu ma1 omega alpha1 beta1 beta2
0.00169063 -0.03683076 0.00013681 0.19696944 0.45766408 0.28640742
Std. Errors:
based on Hessian
Error Analysis:
Estimate Std. Error t value Pr(>|t|)
mu 1.691e-03 9.153e-04 1.847 0.06474 .
ma1 -3.683e-02 2.987e-02 -1.233 0.21756
omega 1.368e-04 3.181e-05 4.301 1.70e-05 ***
alpha1 1.970e-01 3.558e-02 5.536 3.09e-08 ***
beta1 4.577e-01 1.570e-01 2.914 0.00356 **
beta2 2.864e-01 1.358e-01 2.109 0.03494 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Log Likelihood:
2526.187 normalized: 1.804419
Description:
Tue Jul 13 02:21:14 2021 by user: Henry
Standardised Residuals Tests:
Statistic p-Value
Jarque-Bera Test R Chi^2 707.0289 0
Shapiro-Wilk Test R W 0.9530929 0
Ljung-Box Test R Q(10) 17.48786 0.06424225
Ljung-Box Test R Q(15) 20.20186 0.164325
Ljung-Box Test R Q(20) 23.6744 0.2569046
Ljung-Box Test R^2 Q(10) 6.571882 0.7651488
Ljung-Box Test R^2 Q(15) 8.050817 0.9217292
Ljung-Box Test R^2 Q(20) 12.63901 0.8923298
LM Arch Test R TR^2 6.81881 0.8693513
Information Criterion Statistics:
AIC BIC SIC HQIC
-3.600267 -3.577792 -3.600304 -3.591866The results of Jarque-Bera Test and Shapiro-Wilk Test also confirm the observation based on the QQ plot. Both of the tests have the Null hypothesis of normality. By rejecting the Null hypothesis, the Normality assumption does not hold for the ARMA-GARCH model that we fit. Considering that the sum of beta1 and alpha1 is smaller than 1, the choice of ARMA-GARCH model itself is a good fit for the data. An ARMA-GARCH model that relies on non-normal conditional distribution assumptions may be considered.
t and Skewed t distribution
Title:
GARCH Modelling
Call:
garchFit(formula = ~arma(0, 1) + garch(1, 2), data = data_bitcoin$log_return,
cond.dist = "std", trace = F)
Mean and Variance Equation:
data ~ arma(0, 1) + garch(1, 2)
<environment: 0x0000000025545558>
[data = data_bitcoin$log_return]
Conditional Distribution:
std
Coefficient(s):
mu ma1 omega alpha1 beta1 beta2
1.6033e-03 -2.9932e-02 7.2494e-05 2.0261e-01 5.7506e-01 2.6223e-01
shape
2.8165e+00
Std. Errors:
based on Hessian
Error Analysis:
Estimate Std. Error t value Pr(>|t|)
mu 1.603e-03 7.110e-04 2.255 0.02413 *
ma1 -2.993e-02 2.338e-02 -1.280 0.20047
omega 7.249e-05 3.483e-05 2.081 0.03742 *
alpha1 2.026e-01 6.995e-02 2.897 0.00377 **
beta1 5.751e-01 2.562e-01 2.244 0.02482 *
beta2 2.622e-01 2.286e-01 1.147 0.25138
shape 2.817e+00 2.705e-01 10.412 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Log Likelihood:
2640.862 normalized: 1.88633
Description:
Tue Jul 13 02:21:15 2021 by user: Henry
Standardised Residuals Tests:
Statistic p-Value
Jarque-Bera Test R Chi^2 966.6385 0
Shapiro-Wilk Test R W 0.9475479 0
Ljung-Box Test R Q(10) 18.82456 0.04254842
Ljung-Box Test R Q(15) 21.36228 0.1256481
Ljung-Box Test R Q(20) 24.50358 0.2210866
Ljung-Box Test R^2 Q(10) 6.762055 0.7477012
Ljung-Box Test R^2 Q(15) 8.305742 0.9109409
Ljung-Box Test R^2 Q(20) 12.32491 0.9044391
LM Arch Test R TR^2 7.367162 0.8324273
Information Criterion Statistics:
AIC BIC SIC HQIC
-3.762659 -3.736438 -3.762709 -3.752857
Title:
GARCH Modelling
Call:
garchFit(formula = ~arma(0, 1) + garch(1, 2), data = data_bitcoin$log_return,
cond.dist = "sstd", trace = F)
Mean and Variance Equation:
data ~ arma(0, 1) + garch(1, 2)
<environment: 0x0000000013a028c8>
[data = data_bitcoin$log_return]
Conditional Distribution:
sstd
Coefficient(s):
mu ma1 omega alpha1 beta1 beta2
0.0017561 -0.0299459 0.0000732 0.2035925 0.5724181 0.2637382
skew shape
1.0083309 2.8191250
Std. Errors:
based on Hessian
Error Analysis:
Estimate Std. Error t value Pr(>|t|)
mu 1.756e-03 9.043e-04 1.942 0.05214 .
ma1 -2.995e-02 2.339e-02 -1.281 0.20035
omega 7.320e-05 3.511e-05 2.085 0.03707 *
alpha1 2.036e-01 7.002e-02 2.907 0.00364 **
beta1 5.724e-01 2.539e-01 2.255 0.02416 *
beta2 2.637e-01 2.263e-01 1.165 0.24387
skew 1.008e+00 3.061e-02 32.946 < 2e-16 ***
shape 2.819e+00 2.711e-01 10.398 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Log Likelihood:
2640.899 normalized: 1.886356
Description:
Tue Jul 13 02:21:16 2021 by user: Henry
Standardised Residuals Tests:
Statistic p-Value
Jarque-Bera Test R Chi^2 964.7639 0
Shapiro-Wilk Test R W 0.9475876 0
Ljung-Box Test R Q(10) 18.83047 0.04246958
Ljung-Box Test R Q(15) 21.37271 0.1253377
Ljung-Box Test R Q(20) 24.52423 0.2202424
Ljung-Box Test R^2 Q(10) 6.7669 0.7472525
Ljung-Box Test R^2 Q(15) 8.307037 0.910884
Ljung-Box Test R^2 Q(20) 12.34609 0.903649
LM Arch Test R TR^2 7.376748 0.8317459
Information Criterion Statistics:
AIC BIC SIC HQIC
-3.761284 -3.731317 -3.761349 -3.750082
Although we see a better QQ plot for both the t-distribution and the skewed t-distribution ARMA-GARCH models, the Ljung-Box test on Q(10) has rejected its Null Hypothesis, meaning that there is at least one autocorrelation greater than zero between the residuals for a set of time lags. In the other words, both of the models do not fully capture the autocorrelation from the data. Thus, although the two models have a better qqplot, the ARMA GARCH model under the normal conditional distribution will be used in forecasting.
Prediction
From both of the plots, the volatility of BTC Daily Log Return is continuously increasing in recent days, and it is going to keep increasing for at least the next ten days. Because of the dissatisfication of the assumptions for ARMA-GARCH model, some other types of models may be considered for a more accurate prediction on Bitcoin properties. An alternative model would be the LSTM model.
LSTM
Long Short Term Memory networks (LSTMs) see ubiquitous use in processing and making predictions based on time series data and are designed to extend standard Recurrent Neural Networks (RNNs) by avoiding the long-term dependency problem. Standard RNNs, though capable of connecting previous information to the present task, struggle to connect this previous information if presented too far in the past due to vanishing or exploding gradients in the propagation. The LSTM consists of input, hidden, and output layers, where the fully self-connected hidden layer avoids the long-term dependency problem with its memory cells that guarantee constant error flow within their constant error carousels (CECs). The information encoded in the cell states is carefully regulated by three gates: the input, output, and forget gates, which provide continuous analogues of write, read, and reset operations. Through these gates, a cell state’s relevance in predicting the next value can be continuously updated. The combination of LSTM memory cells’ constant error flow and the three gate operations allow us to make long-term dependent predictions, independent of stationarity or distribution assumptions.
In our LSTM model to predict and forecast BTC daily log return volatilities, we utilized PyTorch’s LSTM class and Adam optimizer, with a hidden size of 70, sequence length of 5, and a learning rate of 4e-5. Then, we split the data 70-30 so that the model could be trained on the first 70% of the log returns to predict the last 30% of the log returns. After training for 8000 epochs, we obtained a training loss of 0.000236815 and prediction loss of 0.002121. Finally, we forecasted 10 days of log return volatilities by feeding the last sequence of the data back into the model to obtain another prediction, appending this prediction to the sequence, and removing the head of the sequence to obtain another sequence of the same length, which can then be used to obtain further predictions in a similar manner. Below are plots of the LSTM prediction and forecast results:
Discussion
Because of the dissatisfaction of the assumptions for Bitcoin modeling that is generally used in the stock market, it is likely that the Bitcoin price would have a different mechanism from that of the stocks. Thus, some other types of models may be considered for a more accurate prediction on Bitcoin properties. Moreover, the coefficients that we chose for the ARMA-GARCH model is not absolute. We used no more than 2 time lag in the model, ARMA(0,1)-GARCH(1,2), but 2 or more time lag is still possible to have a better fit to the given data.
Conclusion
Based on the results of the two models, the volatility of the Bitcoin daily log return is continuously increasing. Since there were certain assumptions that do not hold for the ARMA-GARCH model we picked, we would agree that our forecast would not be the most accurate one. However, the result of the LSTM model confirms our conclusion. Considering the Chinese government’s action against the Bitcoin market in the past few weeks and the fact that China is one of the biggest markets for cryptocurrency, the prediction we have made seems plausible. Thus, we conclude that the daily Bitcoin log return becomes more volatile; and considering its importance to the cryptocurrency market, the market itself may become more volatile.
Note: All codes are set as echo = FALSE and are not shown in the report